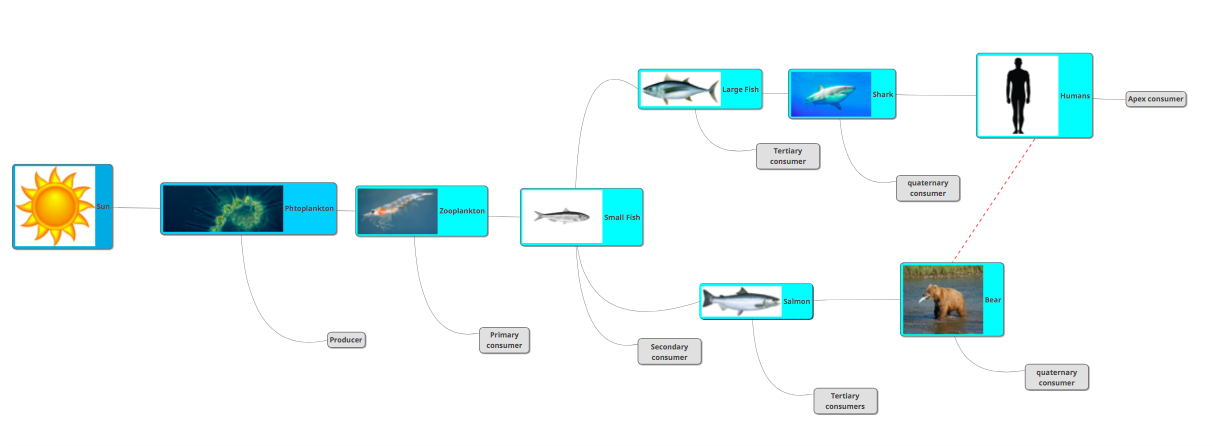
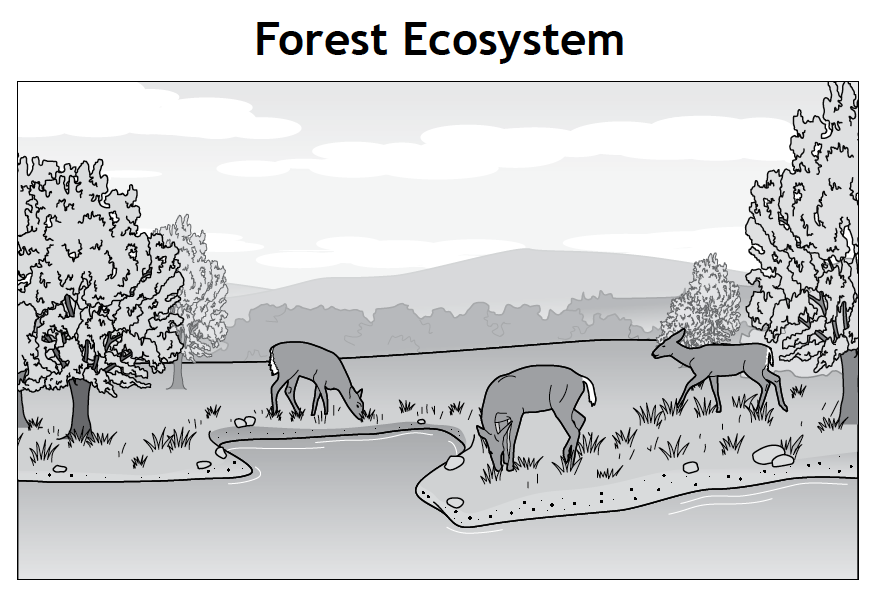
Lake Ecosystem INTERACTIONS
Lake Ecosystem INTERACTIONS
One of the things about space is that there is no gravity! Gravity is the invisible force that pulls you to the center of the earth. My support that there is no gravity in space is that space has no density, because of this, space has no gravity. Space is only the empty(emptiness has no density, which exerts no gravity) space between celestial bodies(including Earth). Technically there is gravity in space because all of the celestial bodies exert a certain amount of gravitational force, it affects all within it's vicinity, pulling the objects to it's center/core. But the farther you get away from the celestial body the less the gravity affects you. But the closer you get to another planet that planet's gravity grows, and eventually that planet's gravity wins over the farther planet's gravity because you are closer to that planet.
Taking off was hard, it was hard because we needed to find the escape velocity. Escape velocity is a certain speed that is used to escape a certain field of gravity. Our escape velocity was 11.2 k/s to escape earth's gravity, Earth's gravity is 9.8 meters per second. The takeoff used a lot of fuel, and it was very loud! I used ear plugs! We had jobs that we were supposed to do. My job is to be a doctor and be a pediatric(I recommend medicines to people). Other people's jobs were the hydroponic gardener(grew plants in water), the fitness trainer(so that we didn't have muscle failure), the cook. We also had a plumber so that we cold get rid of waste and so that he controls our water supply. We also chose a constitutional monarchy(we chose a king that is contained by the constitution. We also had a tailor so that we had new clothes to wear so we didn't grow out of them. What do I already know about Mars?
|
Amir RajaI am Amir Raja, a doctor from Kuala Lumpur, Malaysia. It would be very important to have a doctor along on the first manned mission to Mars because you would need someone to help you when you have an injury or if we encounter any foreign diseases. I am excited for this trip because it would be exciting to start a foothold for humanity, on mars. Archives
May 2017
Categories |
| What's going on in Mr. Solarz' Class? |
|















 RSS Feed
RSS Feed
